-- 對數
 。
。
當x和β進一步限制為正實數的時候,對數是一個唯一的實數。
例如,因為
 ,
,
我們可以得出
 ,
,
用日常語言說,以3為基81的對數是4。
對數函數
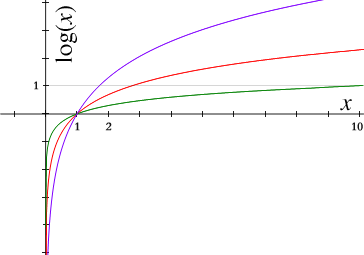
函數logβ(x)依賴於β和x二者,但是術語對數函數在標準用法中用來稱呼形如logβ(x)的函數,在其中基β是固定的而只有一個參數x。所以對每個基 的值(必須是正數及不是1)只有唯一的對數函數。從這個角度看,基β的對數函數是指數函數y = βx的反函數。詞語「對數」經常用來稱呼對數函數自身和這個函數的一個特定值。
的值(必須是正數及不是1)只有唯一的對數函數。從這個角度看,基β的對數函數是指數函數y = βx的反函數。詞語「對數」經常用來稱呼對數函數自身和這個函數的一個特定值。
 的值(必須是正數及不是1)只有唯一的對數函數。從這個角度看,基β的對數函數是指數函數y = βx的反函數。詞語「對數」經常用來稱呼對數函數自身和這個函數的一個特定值。
的值(必須是正數及不是1)只有唯一的對數函數。從這個角度看,基β的對數函數是指數函數y = βx的反函數。詞語「對數」經常用來稱呼對數函數自身和這個函數的一個特定值。對數函數圖像和指數函數圖像關於直線y=x對稱(互為反函數)。
對數函數的性質有:
常用公式
- 基本

- 和差
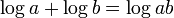

- 指係


- 換底
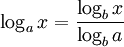
- 還原
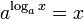
- 互換

- 倒數

- 次方
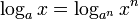
- 連鎖

有理和無理指數
 。
。
對數可以簡化乘法運算為加法,除法為減法,冪運算為乘法,根運算為除法。所以,在發明電子計算機之前,對數對進行冗長的數值運算是很有用的,它們廣泛的用於天文、工程、航海和測繪等領域中。它們有重要的數學性質而在今天仍在廣泛使用中。
底數
最常用做底數的是10、數學常數e ≈ 2.71828...和2。當寫出不帶底數的「log」的時候,意圖要從上下文中確定:
- 自然對數 (loge, ln, log或Ln)在數學分析中。
- 常用對數 (log10或簡寫為log;有時為lg)在工程中和在使用對數表簡化計算的時候。
- 二進制對數 (log2;有時寫為lg或lb)在資訊理論和音程中。
- 不確定對數在底數無關緊要的時候,比如計算複雜性理論用大O符號描述演算法的漸進行為的時候。
為了避免混淆,在可能有歧義的時候最好指定底數。
[編輯]換底數
儘管有很多有用的恆等式,對計算器最重要的是找到不是建造於計算器內的底數(通常是loge和log10)的其他底數的對數。要使用其他底數β找到底數α的對數:
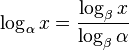 。
。
此外,這個結果蘊涵了所有對數函數(不管什麼底數)都是相互類似的。所以用計算器計算16的底數2的對數:
 。
。
[編輯]對數的用途
對數對解冪是未知的方程是有用的。它們有簡單的導數,所以它們經常用在解積分中。對數是三個相關的函數中的一個。在等式bn = x中,b可以從x的n次方根,n從x 的b底數的對數,x從b的n次的冪來確定。參見對數恆等式得到掌控對數函數的一些規則。
[編輯]簡便計算
對數把注意力從平常的數轉移到了冪。只要使用相同的底數,就會使特定運算更容易:
| 數的運算 | 冪的運算 | 對數恆等式 |
|---|---|---|
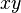 | 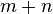 |  |
 | 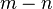 | 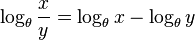 |
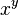 |  |  |
![\sqrt[y]{x}](http://upload.wikimedia.org/math/8/9/b/89b0836496d5a0309973d558fd8bd48c.png) |  | ![\log_{\theta}\sqrt[y]{x}=\frac{\log_{\theta}x}{y}](http://upload.wikimedia.org/math/d/c/5/dc5eaab05c0c70592f5486f6514e25d3.png) |
這些關係使在兩個數上的這種運算更快,在乘法計算器出現之前正確的使用對數是基本技能。
[編輯]群論
從純數學的觀點來看,恆等式
- logab = loga + logb,
對數函數是從正實數的乘法群到實數的加法群的唯一連續同構。
沒有留言:
張貼留言