-- 指數函數
作為實數變量 x 的函數,y=ex 的圖像總是正的(在 x 軸之上)並遞增(從左向右看)。它永不觸及 x 軸,儘管它可以任意程度的靠近它(所以,x 軸是這個圖像的水平漸近線。它的反函數是自然對數 ln(x),它定義在所有正數 x 上。
有時,特別是在科學中,術語指數函數更一般性的用於形如 kax 的函數,這裡的 a 叫做「底數」,是不等於 1 的任何正實數。本文最初集中於帶有底數為歐拉數 e 的指數函數。
性質
最簡單的,指數函數按恆定速率翻倍。例如細菌培養時細菌總數(近似的)每三個小時翻倍,和汽車的價值每年減少 10% 都可以被表示為一個指數。
使用自然對數,你可以定義更一般的指數函數。函數
定義於所有的 a > 0,和所有的實數 x。它叫做底數為 a 的指數函數。注意這個 ax 的定義依賴於先前確立的定義於所有實數上的函數 ex 的存在。(這裡我們先既不在形式上的也不概念上明確這樣一個函數是否存在,或非自然指數意味着什麼。)
注意上述等式對於 a = e 成立,因為
指數函數可「在加法和乘法之間轉換」,在下列「指數定律」的前三個和第五個中表述:
對於任何 a > 0,實數 b,和整數 n > 1:
指數爆炸
指數爆炸是指指數函數的增加過程中,初始時十分緩慢,但逐步加速,以至於其函數圖像將會與y軸平行。


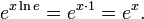
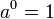
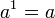
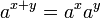
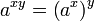

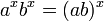
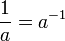
![\sqrt[n]{a^b} = \left(\sqrt[n]{a}\right)^b = a^{b/n}.](http://upload.wikimedia.org/math/8/2/1/821704e8992ee67a4d8988774e23bcb8.png)
沒有留言:
張貼留言