- 二次函數
在實係數一元二次方程中,若a、b中出現無理數,則即使Δ為完全平方數,求得的根也有可能出現無理數的情況。Why
頂點
拋物線的頂點是它轉彎的地方,也稱為駐點。如果二次函數是標準形式,則頂點為 。用配方法,可以把一般形式
。用配方法,可以把一般形式 化為:
化為: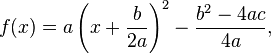
因此在一般形式中,拋物線的頂點是:
在實係數一元二次方程中,若a、b中出現無理數,則即使Δ為完全平方數,求得的根也有可能出現無理數的情況。Why
頂點
拋物線的頂點是它轉彎的地方,也稱為駐點。如果二次函數是標準形式,則頂點為 。用配方法,可以把一般形式
。用配方法,可以把一般形式 化為:
化為: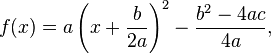
因此在一般形式中,拋物線的頂點是:
在實係數一元二次方程中,若a、b中出現無理數,則即使Δ為完全平方數,求得的根也有可能出現無理數的情況。Why
頂點
拋物線的頂點是它轉彎的地方,也稱為駐點。如果二次函數是標準形式,則頂點為 。用配方法,可以把一般形式
。用配方法,可以把一般形式 化為:
化為: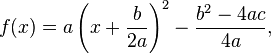
因此在一般形式中,拋物線的頂點是:
在實係數一元二次方程中,若a、b中出現無理數,則即使Δ為完全平方數,求得的根也有可能出現無理數的情況。Why
頂點
拋物線的頂點是它轉彎的地方,也稱為駐點。如果二次函數是標準形式,則頂點為 。用配方法,可以把一般形式
。用配方法,可以把一般形式 化為:
化為: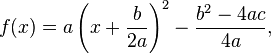
因此在一般形式中,拋物線的頂點是:
拋物線的頂點是它轉彎的地方,也稱為駐點。如果二次函數是標準形式,則頂點為 。用配方法,可以把一般形式
。用配方法,可以把一般形式 化為:
化為:
 。用配方法,可以把一般形式
。用配方法,可以把一般形式 化為:
化為: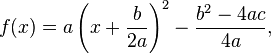
因此在一般形式中,拋物線的頂點是:



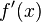 的根:
的根:

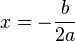
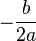 是
是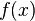 的
的 值。現在,為了求出
值。現在,為了求出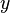 ,我們把
,我們把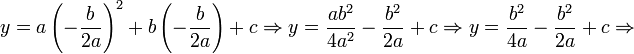
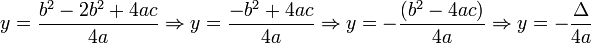



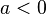
沒有留言:
張貼留言