- 一元二次方程
例如,x2 − 3x + 2 = 0,![\left (3-2i \right)x^2+\sqrt[\pi]{23-6i}x-\sin 2=0](http://upload.wikimedia.org/math/1/0/b/10b667da4a4809da4eec4821ac3d140a.png) ,t2 - 3 = 0等都是一元二次方程。
,t2 - 3 = 0等都是一元二次方程。
![\left (3-2i \right)x^2+\sqrt[\pi]{23-6i}x-\sin 2=0](http://upload.wikimedia.org/math/1/0/b/10b667da4a4809da4eec4821ac3d140a.png) ,t2 - 3 = 0等都是一元二次方程。
,t2 - 3 = 0等都是一元二次方程。 公式解法
對於 ,它的根可以表示為:
,它的根可以表示為:
 ,它的根可以表示為:
,它的根可以表示為:根的判別式
對於實係數一元二次方程 ,
, 稱作一元二次方程根的判別式。根據判別式,一元二次方程的根有三種可能的情況:
稱作一元二次方程根的判別式。根據判別式,一元二次方程的根有三種可能的情況:- 如果Δ = 0,則這個一元二次方程有兩個相等的實數根。而且這兩個根皆為

- 如果Δ < 0,[(Δ < 0)與(Δ > 0)],正負號相反,則這個一元二次方程有兩個不同的複數根。這時根為

 ,
, 稱作一元二次方程根的判別式。根據判別式,一元二次方程的根有三種可能的情況:
稱作一元二次方程根的判別式。根據判別式,一元二次方程的根有三種可能的情況:

根與係數
根據韋達定理可以找出一元二次方程的根與方程中係數的關係。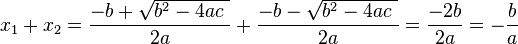

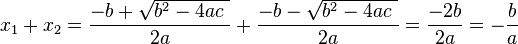

圖像解法
另外一種解法是把一元二次方程ax2 + bx + c = 0化為 的形式。
的形式。
則方程ax2 + bx + c = 0的根,就是函數 和
和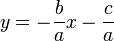 交點的X坐標。通過作圖,可以得到一元二次方程根的近似值。
交點的X坐標。通過作圖,可以得到一元二次方程根的近似值。
 的形式。
的形式。 和
和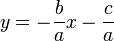 交點的X坐標。
交點的X坐標。計算機法
在使用計算機解一元二次方程時,跟人手工計算類似,大部分情況下也是根據下面的公式去解
可以進行符號運算的程序,比如Mathematica, 可以給出準確的解析表達式。而大部分程序則只會給出數值解。(但亦有部份顯示平方根及虛數)



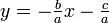 交點的X座標
交點的X座標
沒有留言:
張貼留言